Sumário
- Support Vector Machines (SVMs)
- Kernel Trick
- Formulação Final
- Como pensar em Kernel de nós e Diffusion Kernel
Support Vector Machines (SVMs)
Support Vector Machines são uma das minhas ideias favoritas no contexto de Aprendizado de Máquina. É um conceito muito simples que combinado com matemática, se torna uma ferramenta poderosa. O cientista soviético Vladimir Vapnik trouxe a ideia original nos anos 60 mas apenas em 1992, um grupo de cientistias foram capazes de encontrar um truque que transformasse o modelo linear em não linear.
Imagine duas classes separáveis que vivem em um espaço qualquer. Para criar um modelo, devemos encontrar a melhor maneira de separá-los. Enquanto Árvores de Decisão e Redes Neurais tem suas ideias, SVM buscam encontrar uma faixa que realize a melhor separação.
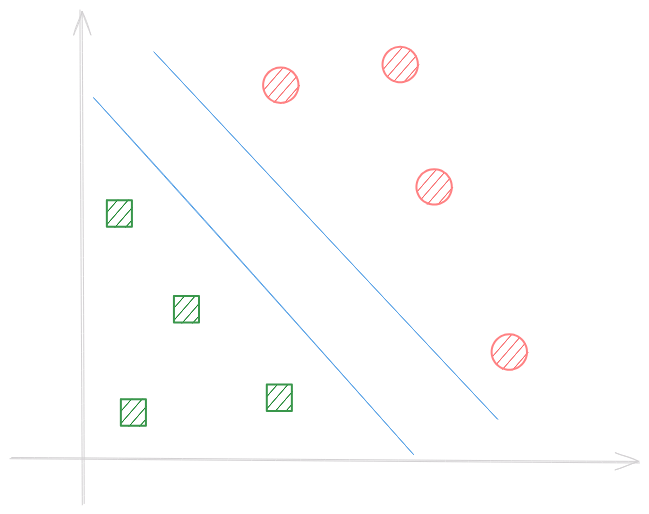
A faixa tem duas bordas e nós queremos maximizar a distância entre elas.
Regra de Decisão
Considere \(\vec{w}\) um vetor perpendicular a faixa e considere que queremos classificar um novo exemplo \(\vec{u}\). Nosso objetivo é checar se \(\vec{u}\) pertence ao lado direito ou esquerdo da faixa. Para tanto, nós devemos projetar \(\vec{u}\) em \(\vec{w}\)
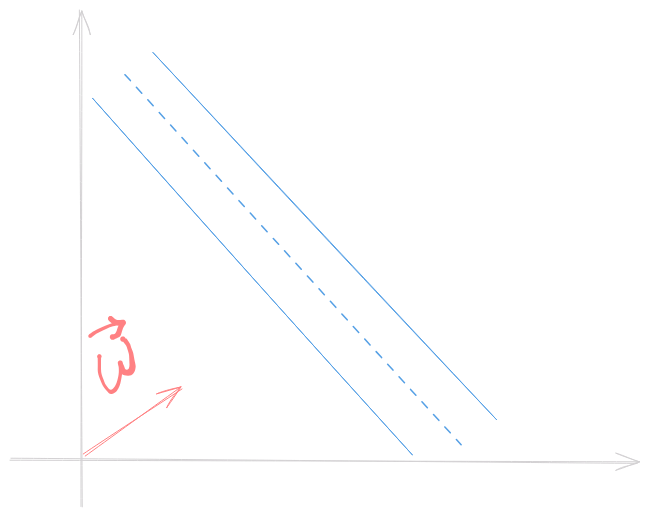
Assim, para classificar \(\vec{u}\) entre classe 1 ou 2, checamos se \(\vec{w} \vec{u} \ge c\), onde \(c\) is a constant. Considerando \(c=-b\), podemos escrever uma regra de decisão:
Se \(\vec{w} \vec{u} + b \ge 0\) então \(\vec{u}\) pertence a classe 1.
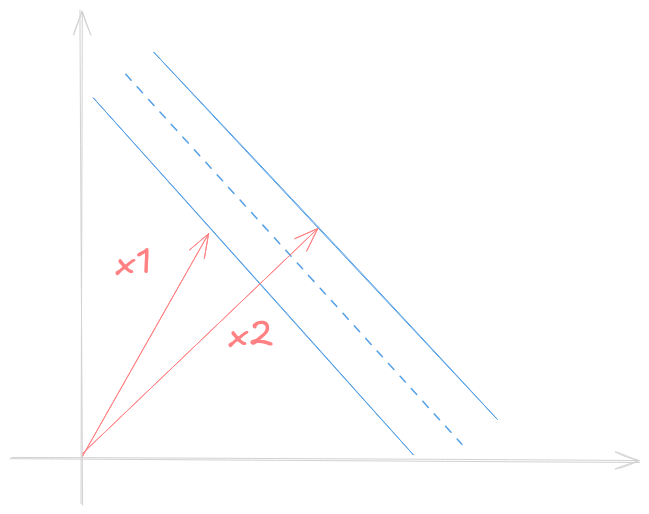
Ótimo! Mas ainda não sabemos qual valor usar, então devemos introduzir algumas restrições (constraints) a fim de calcular \(\vec{w}\) e \(b\). Considere \(x_1\), \(x_2\) amostras de classe 1 e 2 respectivamente. Assim, \[ \begin{cases} \vec{w} \vec{x_1} + b \ge 1 \\\ \vec{w} \vec{x_2} + b \le 1 \end{cases} \]
Para conveniência introduzimos \(y\) de forma que \[ \begin{cases} x_1 \implies y_i = 1 \\\ x_2 \implies y_i = -1 \end{cases} \] Assim reescrevemos (1) com \(y_i\) dos dois lados: \[ y_i (\vec{w} \vec{x_i} + b) \ge 1 \] Note que amostras nas bordas da faixa tem \[ y_i (\vec{w} \vec{x_i} + b) = 1 \]
Encontrando a faixa mais larga
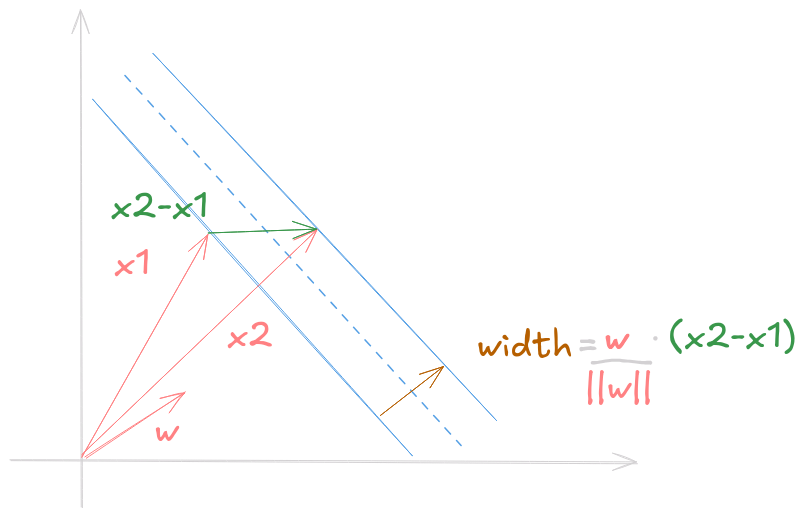
Sabendo a equação para amostras nas bordas, podemos encontrar a largura da faixa ao projetar a diferença entre os representantes de cada classe nas boardas pela vetor perpendicular a faixa normalizado.
O vetor perpendicular que buscamos é \(\dfrac{\vec{w}}{||\vec{w}||}\) e a diferença \((x_1 - x_2)\). Portanto, a largura da faixa é dada por \(\text{width} = \dfrac{\vec{w}}{||\vec{w}||}(x_1 - x_2)\).
Reescrevendo (1) para amostras nas bordas obtemos \[ \begin{cases} \vec{x_1} = \dfrac{1 - b}{\vec{w}} \\\ \vec{x_2} = - \dfrac{1 - b}{\vec{w}} \end{cases} \]
E substituindo na fórmula da largura \[ \text{width} = \dfrac{\vec{w}}{||\vec{w}||}(\dfrac{1 - b}{\vec{w}} + \dfrac{1 - b}{\vec{w}}) = \dfrac{2}{||\vec{w}||} \]
Nós queremos maximizar a largura, isto é, maximizar \(\dfrac{2}{||\vec{w}||}\). De forma mais conveniente, podemos minimizar \(\dfrac{1}{2}||\vec{w}||^2\).
Otimização com Multiplicadores de Lagrange
Para minimizar \(\dfrac{1}{2}||\vec{w}||^2\) com as restrições \(y_i (\vec{w} \vec{x_i} + b) - 1 \ge 0\) (as quais garantem que cada amostra estará do lado correto) podemos utilizar Multiplicadores de Lagrange. O Lagrangiano é uma expressão da forma \(L(x, \lambda) = f(x) - \lambda g(x)\). O valor mínimo é encontrado quando pegamos as derivadas parciais e igualamos a 0. \[ L = \dfrac{1}{2}||\vec{w}||^2 - \sum_l a_i (y_i (\vec{x_i}\vec{w} + b) - 1) \] Introduzimos \(\alpha s\) para cada amostra. A soma é realizada sobre o conjunto de amostras \(l\).
Note que \(\frac{\partial ||\vec{w}||}{\partial \vec{w}} = \frac{\vec{w}}{||\vec{w}||}\).
Ao pegar as derivadas parciais obtemos \[ \dfrac{\partial{L}}{\partial{\vec{w}}} = \vec{w} - \sum_l a_i y_i \vec{x_i} = 0 \implies \vec{w} = \sum_l a_i y_i \vec{x_i} \\\ \dfrac{\partial{L}}{\partial{b}} = \sum_l a_i y_i = 0 \]
Resumindo, encontramos que o vetor \(\vec{w}\) é uma combinação linear das amostras. Podemos substituir as expressões obtidas em L para encontrar:
\[ L = \dfrac{1}{2}(\sum_l a_i y_i \vec{x_i}) (\sum_l a_j y_j \vec{x_j}) - (\sum_l a_i y_i \vec{x_i}) (\sum_l a_j y_j \vec{x_j}) + \sum_l a_i \]
\[ L = \sum_l a_i - \dfrac{1}{2}(\sum_l a_i a_j y_i y_j \vec{x_i} \vec{x_j}) \]
Finalmente! O mais importante aqui é descobrirmos que a otimização depende apenas do produto escalar dos pares de amostras (\(\vec{x_i} \vec{x_j}\)).
Podemos inserir o vetor obtido para a faixa \(\vec{w} = \sum_l a_i y_i \vec{x_i}\) para encontrar uma nova regra de decisão:
Se \(\sum_l a_i y_i \vec{x_i} \vec{u} + b \ge 0\) então \(\vec{u}\) pertence a classe 1.
De forma similar, a regra de decisão também depende apenas do produto escalar entre o vetor desconhecido e as amostras.
Nota 1: é possível provar que o Lagrangiano pertence a um espaço convexo, e portanto, o máximo local também é global.
Nota 2: as amostras com \(\alpha_i \ne 0\) serão aquelas nas bordas da faixa.
Kernel
Uma forma comum para lidar com a linearidade de um vetor \(\vec{u}: R^m\) é criar uma função \(\phi(x): R^m \rightarrow R^n\) com \(n \ge m\) em que as novas coordenadas \(\phi(u)\) serão dadas por funções não lineares. Esse processo pode ser computacionalmente pesado, especialmente em altas dimensões.
Entretanto, como visto nos últimos parágrafos, para otimizar e classificar precisamos apenas do resultado de \(u\cdot v\) ou \(\phi(u)\cdot \phi(v)\). O Kernel Trick é que nós não precisamos de uma função \(\phi\), apenas de uma função que calcule o resultado de \(\phi(u)\phi(v)\). Essa função é o kernel, representado pela letra \(k\).
\[ k(u,v)=\phi(u)\phi(v) \]
Kernel RBF
O Kernel Radial Basis Function (RBF), generaliza um kernel polinomial para gerar a relação entre vetores num espaço de dimensão infinita: \[ k(u,v)=\exp{(-\lambda ||\vec{u} \cdot \vec{v}||)} \]
Formulação Final
Considere um conjunto de amostras \(x\), um kernel \(k\). Uma nova amostra \(\vec{u}\) é classificada usando
\[ \text{sgn}(\sum_l a_i y_i k(\vec{x_i}, \vec{u}) + b) \]
onde \(\vec{\alpha}\) resolve
\[ \begin{cases} \text{argmin}_{\vec{\alpha}} \sum_l a_i - \dfrac{1}{2}(\sum_l a_i a_j y_i y_j k(\vec{x_i},\vec{x_j})) \newline \sum_l a_i y_i = 0 \end{cases} \]
Inferência em Grafos
Em ciência de dados, os dados podem estar estruturados como nós de um grafo e não como vetores. Isso pode acontecer naturalmente, pela discretização de um espaço contínuo ou por que é conveniente.
Para aplicar SVMs em grafos, é preciso encontrar um \(k(u, v)\) entre os nós.
Matriz de Adjacência
Não é um kernel válido :( Podemos encontrar vários problemas. Um exemplo muito claro é que nem todos vértices podem ser diretamente alcançáveis.
Difusão em Grafos
Para resolver esse problema, utilizamos a difusão em grafos. A difusão é um processo amplamente conhecido na física e pode ser interpretado como o espalhamento de uma substância quando introduzido em um meio.
Na versão para grafos, a difusão pode ser considerada como um RBF em grafos e representa caminhadas aleatórias em tempo contínuo. \[ K=\exp (\Delta) \]
onde \(\Delta\) é o Laplaciano da matriz de adjacência.